「中点連結定理? 名前からして難しそう……」
「台形の問題、どこに線を引けばいいか全然わからない!」
テスト前なのに、教科書の説明を読んでも頭に入ってこなくて、焦っていませんか?
図形問題って、ひらめきが必要な気がして、苦手な人にとっては本当に苦痛ですよね。
でも、安心してください。
中点連結定理は、実は中学数学で一番「使い勝手がいい」便利な道具なんです。
特に、多くの人がつまずく「台形」の問題。
これも、たった一本の線を引くだけで、簡単な「三角形」の問題に早変わりします。
この記事では、偏差値40台から数々の生徒を合格させてきた私が、図形問題を「パズル」のように解くための「魔法の補助線」の引き方を伝授します。
これを読めば、テストで台形が出た瞬間、「ラッキー!」と思えるようになりますよ。
[著者情報]
この記事を書いた人:西田 武(にしだ たけし)
中学数学専門・家庭教師
「数学が苦手なのは君のせいじゃない、教え方が悪いだけ」をモットーに、図形問題をパズルのように解くメソッドを開発。偏差値40台の生徒を多数、難関公立高校へ合格させた実績を持つ。
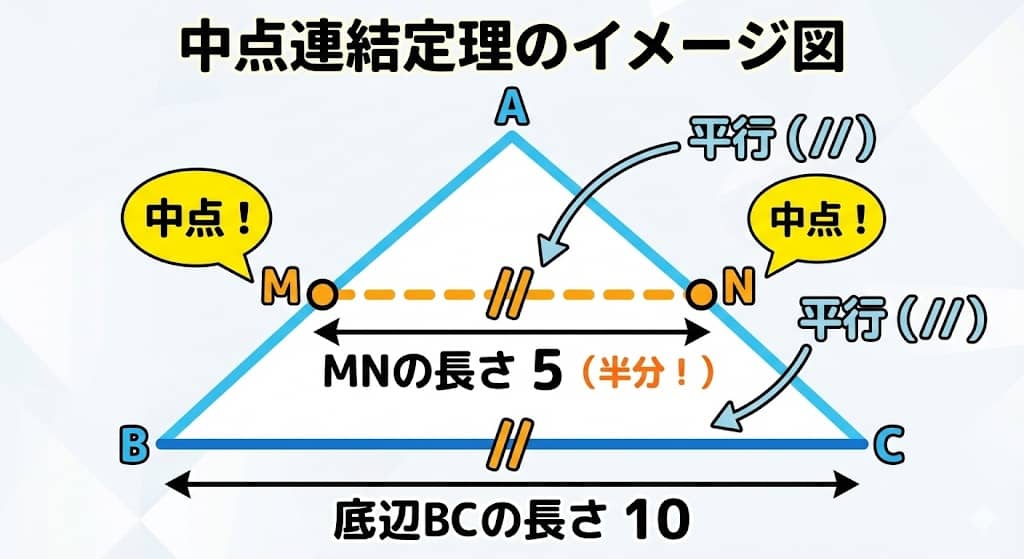
30秒で理解! 中点連結定理は「真ん中・平行・半分」の3点セット
まずは、定理の中身をサクッと理解しましょう。
教科書の難しい言葉は忘れてください。覚えるのはこれだけです。
「三角形の2つの辺の『真ん中(中点)』を結ぶと、底辺と『平行』になって、長さは『半分』になる」
つまり、「中点×2=発動」です。
三角形の中に中点が2つあったら、自動的にこの魔法が発動すると考えてください。
【証明のコツ】なぜ半分になる? 理由は「1:2のピラミッド」だから
「でも、なんで半分になるの?」
そう疑問に思ったあなたは鋭いです。でも、これは新しい知識ではありません。
実は、あなたがすでに知っている「相似」の知識で説明できるんです。
中点連結定理とは、要するに「相似比が1:2の三角形(ピラミッド型)」のこと。
- 小さい三角形(上)と、大きい三角形(全体)を見比べてください。
- 辺の長さがちょうど2倍になっていますよね?(中点だから1:2)
- だから、底辺の長さも当然1:2、つまり半分になるんです。
そして、「定理の逆」も成り立ちます。
「中点を通って、底辺に平行な線を引いたら、反対側も勝手に中点になる」
これもテストでよく使うので、セットで覚えておきましょう。
【必勝パターン】台形問題は「対角線」一本で瞬殺できる
さあ、ここからが本番です。
テストで一番差がつくのが、この「台形」の問題。
「AD // BC の台形ABCDで、辺ABの中点Mから……」なんて問題文を見ただけで嫌になりますよね。
でも、この必勝パターンを知っていれば大丈夫。
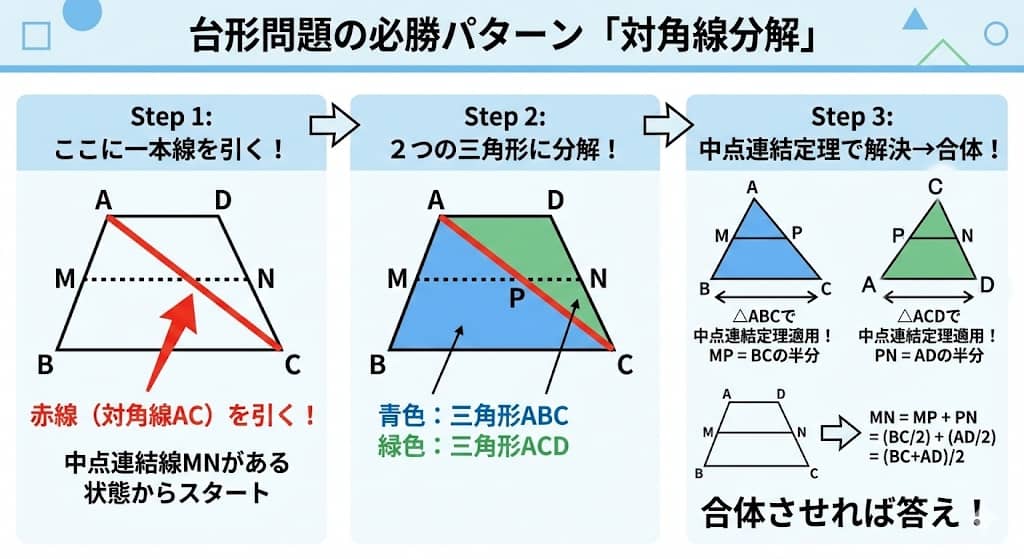
台形の問題が出たら、迷わず「対角線」を引いてください。
手順はたったの3ステップ
- 対角線を引く
台形の対角線(例えばAとCを結ぶ線)を一本引きます。 - 2つの三角形に分解する
すると、台形が「普通の三角形」と「ひっくり返った三角形」の2つに分かれます。 - それぞれで中点連結定理を使う
それぞれの三角形で「長さ半分」のルールを使えば、真ん中の線の長さが簡単に求まります。
✍️ 専門家の経験からの一言アドバイス
【結論】: 補助線は「ひらめき」ではなく「知識」です。
なぜなら、数学が得意な子は「どこに引こうかな?」と悩んでいるのではなく、「台形だから対角線だな」とパターンを当てはめているだけだからです。このパターンを知った今、あなたはもう「数学が得意な子」と同じ武器を持っていますよ。
よく出る応用! 「四角形の中点を結ぶと平行四辺形」の謎解き
最後に、もう一つ頻出のパターンを紹介します。
「どんな四角形でも、各辺の中点を結ぶと平行四辺形になることを証明せよ」
これも、実は「対角線」が鍵なんです。
四角形に対角線を一本引いてみてください。
すると、その対角線を底辺とする「2つの三角形」ができますよね?
- 上の三角形で中点連結定理 → 中点同士を結んだ線は、対角線と平行。
- 下の三角形で中点連結定理 → 中点同士を結んだ線も、対角線と平行。
つまり、向かい合う辺がどちらも「対角線と平行」になるので、結果として互いに平行になり、平行四辺形になるのです。
まるで手品みたいですが、これも「対角線で三角形を作る」という基本ルール通りなんです。
まとめ:図形問題は「ひらめき」じゃなく「パターン」だ
中点連結定理は、難しそうに見えて実はシンプル。
「三角形を見つけるゲーム」だと思ってください。
- 中点×2 = 平行&半分
- 台形が出たら「対角線」
- 四角形も「対角線」
「補助線がひらめかない」と悩む必要はありません。
「台形=対角線」というパターンを知っていれば、テストで必ず解けます。
さあ、自信を持ってテストに挑んでください。健闘を祈ります!
[参考文献リスト]
- 中点連結定理とは?証明や台形の問題の解き方を解説! – Try IT
- 中学校数学教科書(各社)

