[著者情報]
数学のコーチ・アツシ
効率化数学アドバイザー。元大手予備校「逆転合格」専門講師。数学嫌いの運動部員を数多く指導し、平均点以下から80点超えへ導いた実績を持つ。自身も高校時代は部活漬けで、いかに「楽に解くか」を追求した経験から、暗記に頼らない解法のパターン化を提唱している。
「今日の数学の授業で公式が3つも増えて、もう何がなんだか分からない……」
「教科書の例題を見ても、なぜこの公式を使うのかが謎すぎて、解ける気がしない」
佐々木健太さんのように、部活と勉強の両立に励みながら、高校数学の抽象的な壁にぶつかっている方は多いはずです。
特に「三角比の相互関係」が出てきた瞬間、計算の複雑さにフリーズしてしまったのではないでしょうか。
実は、三角比は「暗記」ではなく「仕分け」のゲームです。
公式を丸暗記しようとするからパニックになるのであって、問題文のヒントから「正解の道具」を秒速で選ぶコツさえ掴めば、計算は驚くほど楽になります。
この記事では、予備校講師の視点から、公式を覚える手間を最小限にし、定期テストで確実に平均点以上をもぎ取るための「公式選択フローチャート」を伝授します。
この記事を読み終える頃には、三角比が「攻略可能なパズル」に見えているはずです。
なぜ三角比でパニックになるのか?「丸記」を捨てて「パズル」として捉えるコツ
「公式が多すぎる!」……健太さんがそう叫びたくなる気持ち、本当によく分かります。
\sin, \cos, \tan と、アルファベットが並ぶだけで拒絶反応が出ますよね。
でも、ちょっと待ってください。
実は \sin, \cos, \tan は「3人1組のチーム」であり、誰か1人の正体が分かれば、残りのメンバーも芋づる式に正体が判明するパズルのような関係にあります。
数学が得意な人は、これらを別々の公式として暗記しているのではなく、「1つ見つければ全員見つかる」というセット感覚で捉えています。
この「仕分け」の感覚さえ身につければ、パニックは一瞬で消え去ります。
部活の練習メニューと同じで、状況に合わせて最適な動きを選ぶだけ。
まずは「暗記しなきゃ」というプレッシャーを捨てて、パズルを解く準備を始めましょう。
【保存版】どの公式を使うか一瞬で決まる!相互関係の最短計算ルート
三角比の相互関係には3つの主要な公式がありますが、これらをランダムに使おうとするから計算が迷走します。
与えられた値(ヒント)が何かによって、使うべき公式の順番は一意に決まります。
以下のフローチャートに従うだけで、思考停止状態で計算を進めることが可能です。
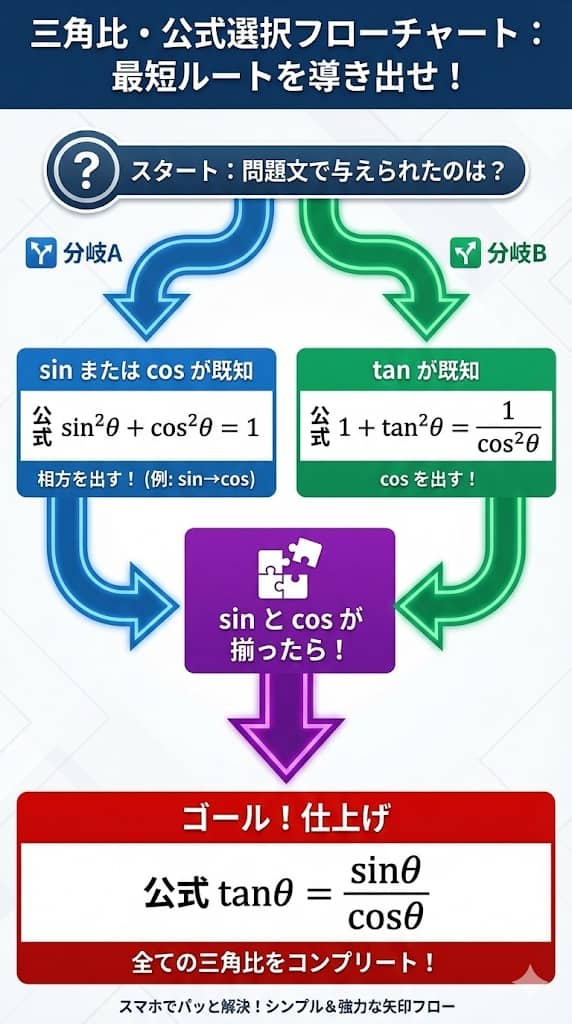
「問題文の条件」と「公式の選択」には、道具と使い道の関係があります。
\sin が分かっているなら、二乗の和が1になる公式を選ぶ。
\tan が分かっているなら、分数を含む公式を選ぶ。
この「仕分け」を徹底するだけで、テストの計算問題は完封できます。
正弦定理・余弦定理の「秒速判別法」|図形問題で迷わないためのキーワード
図形問題に入ると、「正弦定理と余弦定理、どっちを使えばいいの?」という壁にぶつかります。
正弦定理と余弦定理は、図形問題における二大巨頭ですが、実は問題文のキーワードによって使い道が明確に分かれています。
複雑な図形を眺める前に、まずは問題文から以下のキーワードを探してください。
📊 比較表
正弦定理 vs 余弦定理の秒速判別表
| 判別ポイント | 正弦定理 | 余弦定理 |
|---|---|---|
| 最強のキーワード | 「外接円の半径 $R$」 | 「3つの辺」 |
| 図の特徴 | 向かい合う「角と辺」のペアがある | 2辺とその間の角がある |
| 発動条件 | ペアが2セット作れる時 | 辺の情報が圧倒的に多い時 |
「外接円」という言葉が見えたら、考える間もなく正弦定理の出番です。
逆に、辺の長さがたくさん書いてあれば余弦定理を疑いましょう。
この「キーワード検索」を癖にするだけで、公式選びの迷いはゼロになります。
よくある質問:鈍角(90°超え)のマイナス符号でミスしないための最強の視覚化術
- Q. 90°を超える角度(鈍角)になると、プラスかマイナスか分からなくなります。
A. 単位円を「座標」として見てください。\cos は x 座標、\sin は y 座標です。鈍角(左側)に行けば x はマイナスになりますよね? だから 「鈍角の \cos は絶対にマイナス」 なんです。これを丸暗記せず、円の左側に点があるイメージを持つだけで、符号ミスは物理的に防げます。
✍️ 専門家の経験からの一言アドバイス
【結論】: 計算ミスを減らしたいなら、\sin^2 \theta + \cos^2 \theta = 1 の計算をした直後に、必ず「今、角度は鋭角か鈍角か?」を確認する癖をつけてください。
なぜなら、定期テストの失点の多くは、公式の選択ミスではなく、\cos の符号をマイナスにし忘れる「うっかり」だからです。私は多くの部活生を見てきましたが、この「符号チェック」をルーティンに加えるだけで、得点が10点以上安定します。部活の試合で「基本の構え」を確認するのと同じ。数学も最後は「構え」が重要ですよ。
まとめ:公式は選ぶもの。まずは例題1つをフロー通りに解いてみて!
三角比の公式は、健太さんを苦しめるための壁ではなく、問題を解くための「便利な道具」です。
「問題文のヒントを見て、フローチャートから道具を選ぶ」。
この感覚が掴めれば、もうパニックになることはありません。
まずはこの記事のフローチャートを見ながら、教科書の例題を1つだけ「仕分け」してみてください。
「あ、これだけでいいんだ」という感覚が掴めたら、次のテストはもう勝ったも同然です。
応援しています!
[参考文献リスト]
- 高校数学I 三角比の公式まとめと覚え方 – Try IT
- 三角比の相互関係の公式と使い分け – 理系ラボ
- チャート式 基礎からの数学I+A – 数研出版